I am going to talk about mathematics. I am going to wander a bit, going here and there, covering, superficially, a lot of different branches. I don't know each of your backgrounds, but I hope that you will all be able to follow along. The common thread, the thing I will keep coming back to, is a remarkable collection of symbols that has come to be known as Euler's identity. Here is what it looks like:
I guess you could simplify it a bit by subtracting one from each side, giving you this ever so slightly shorter version:
But most of the time it is written the other way. This deceptively simple little formula has an awful lot packed into it. It seems so absurdly improbable, and has so many seemingly unrelated branches of mathematics drawn together into one tiny bundle, that it has acquired almost mystical significance for some people. I once saw it tattooed on a guy's arm at a coffee shop in Central Square. Apparently he isn't the only one. Try doing a google image search for "euler tattoo". By the end of this presentation, I hope you get a sense of why it blows so many people's minds, and why it is true.
Leonhard Euler was a Swiss mathematical genius who lived from 1707-1783. He was extremely prolific, writing tons of books and notes about all kinds of mathematics. He made up a lot of our mathematical notation, and he came up with this identity. (We call it an identity because of the equals sign: it says this is equal to that.)
You can see that our formula has five constants in it. Through them, it unites algebra, geometry, trigonometry, and complex numbers. How can we even begin to interpret it? First, let's go through each of the constants.
I assume that we have a pretty good idea of what 0 and 1 mean.
π is just a regular real number, approximately 3.14. It is the ratio of a circle's circumference to its diameter. That is, if the diameter, the distance across a circle through the center, is 1, then the circumference, the distance around the circle, is π.
If the diameter is 15, the circumference is 15π. People who work in geometry usually like to talk about the radius of a circle more than the diameter. The radius, often abbreviated as r, is half of the diameter. It is the distance from the center of a circle to the rim. So what I've been calling the diameter is more commonly shown as 2r.
Using some tricky geometric proofs, we can show that the area of a circle is π r2, the surface area of a sphere is 4 π r2, the volume of a sphere is 4/3 π r3. π shows up all over the place whenever circles are involved. As I will go into a bit later, π also shows up all over the place whenever we talk about right triangles and trigonometry.
i is the square root of -1.
Most people know that whenever you square a number, the result is positive, even if the number you started with is negative. -3 × -3 = 9. So there really is no such thing as the square root of -1. Nevertheless, when you start doing algebra, after a while you run into equations with solutions, or roots, that are square roots of negative numbers. It took a while, historically, for mathematicians to accept that and to get comfortable with using it. It has been said that in mathematics, you don't understand things, you just get used to them. Eventually, however, mathematicians did get used to the square root of -1, and gave it the name i. i is just a variable that you carry around throughout your equations, with the one simple rule that i2 = -1.
A consequence of that simple rule that will come up later is this
sequence:
i1 = i = i
i2 = i × i = -1
i3 = i × i × i = (i × i) × i = -1 × i = -i
i4 = i × i × i × i = (i × i) × (i × i) = -1 × -1 = 1
i5 = i4 × i = 1 × i = i
i6 = i4 × i2 = 1 × -1 = -1
i7 = i4 × i3 = 1 × -i = -i
and so on.
As you keep multiplying i by itself more times, you go through the progression [i, -1, -i, 1] over and over again forever.
Like π, e is just a regular real number, approximately 2.72. There is a whole book about e that I like a lot called "e: The Story Of A Number" by Eli Maor. It is a book that I wish someone had given me as summer reading when I was about your age. It ranges all over the place and really explains the math and the thinking and people behind the math, rather than just making you memorize stuff and do problems.
Long ago, money lenders working with interest rates figured out the definition of e. The calculusy way of saying it is that e is the limit of (1 + 1/n)n as n goes to infinity. A less mathematically conservative but more intuitive way of saying it is that e = (1 + 1/∞)∞.
In calculus, the idea of a limit is a Big Deal. Basically, you say that the limit of some function of x approaches a limit of a as x approaches b. It's just a way of saying that as this gets closer to this, that gets closer to that. In the above definition of e, we can't actually do math with infinity, but we can say that as n gets closer to infinity (i.e. as it gets bigger), the whole expression will get ever closer to e.
Limits don't just apply to exotic expressions involving infinity. They can apply to ordinary ones too. Take y = 2x. If x is 3, y is 6. If x is 5, y is 10. It is true that the closer x gets to 5, the closer y is going to get to 10, so the limit of 2x as x approaches 5, is 10. This seems like a convoluted way of talking, but as we saw with the definition of e, and in all of calculus, limits really shine.
If you look at the expression (1 + 1/n)n, first look at the part raised to the nth power, that is, 1 + 1/n. It would seem that the bigger n gets, the smaller 1/n gets, and the closer 1 + 1/n gets to being just 1. So you might think that no matter what power you raised that to, as n gets bigger (close to infinity), 1 + 1/n is going to be (infinitely!) close to 1, so the whole thing will be 1, no matter how big the exponent is. Again, to speak in calculus terms, the limit of 1 + 1/n, as n approaches infinity, is 1.
On the other hand, any number greater than 1 (even a little bit) gets bigger as you raise it to more powers. So you might think that (1 + 1/n)n would get infinitely large as n gets large. Either way, you might think that one of them would win: either the exponent getting bigger would push the whole thing to infinity, or the closeness of 1 + 1/n to 1 would push the whole thing to 1. It seems odd, at first, that it ends up being 2.72.
We can get a little sense of this if we just look at the first few
values of n:
n = 1: (1 + 1/1)1 = 21 = 2.0
n = 2: (1 + 1/2)2 = 3/22 = 9/4 = 2.25
n = 3: (1 + 1/3)3 = 4/33 = 64/27 = 2.37
n = 4: (1 + 1/4)4 = 5/44 = 625/256 = 2.44
So we can see that as n increases, it starts at 2 and climbs up from
there, although the steps seem to get smaller the higher we go.
That doesn't prove anything, but it should seem intuitively
plausible that the whole thing ends up at 2.72.
For various reasons, e pops up all over the place in math and science, a lot like π does. We will see some of the reasons for this momentarily.
Given that we have defined e = (1 + 1/n)n as n goes to infinity, we can also manipulate this expression to come up with an equivalent one that might come in handy later. I don't want to get bogged down in the details, so I'm going to throw a lot of terms out and wave my hands a bit. If you don't know about the terms, you can google them, or just not worry about it for now.
You probably already know that
(a + b)2 = a2 + 2ab + b2
and maybe even that:
(a + b)3 = a3 + 3a2b + 3ab2 + b3
There is a pattern here. Since ancient times, people who do algebra
have known that any time you have an expression that looks like
(a + b)n, you can expand it using a diagram called
Pascal's triangle.
Pascal's triangle
is easy to write out, and each row gives the coefficients for
successively higher powers of (a + b). So to write the expanded
version of (a + b)17, you just look at row 17 of
Pascal's triangle and bang it out mindlessly.

The problem is that even though Pascal's triangle is easy to write, the diagram itself literally gets big. In order to know what row 17 should be, you have to write out all 16 rows before it. You could get a computer to do it, but still. At some point, mathematicians figured out a way to write any row of Pascal's triangle without writing all the rows above it. The formula they use for this is called the binomial formula. Now we can figure out how to expand (a + b)17 all by itself.
I'm sorry, but this is one of those places where I just have to ask you to trust me. I'm not going to get into the details of how they figured out the binomial formula, or even what it looks like, but if you are interested, you can see a slightly technical proof and discussion of all this on the Wikipedia page of the binomial theorem.
So now we have this binomial formula that tells us how to expand (a + b)n, and we also know that e = (1 + 1/n)n. So why don't we let a = 1 and b = 1/n in the binomial formula? If we do that, it shows us that as n goes to infinity, the first several terms of the expansion of (1 + 1/n)n look like this after a little bit of algebra:
I assume you know that the exclamation point means
factorial, and what that means:
n! = n × (n-1) × (n-2) × ... × 1
so:
4! = 4 × 3 × 2 × 1 = 24
This means that in addition to our old definition of e:
e = (1 + 1/n)n (as n goes to infinity)
we also have this new definition:
e = 1 + 1 + 1/2! + 1/3! + ...
This is noteworthy for two reasons. First, this new definition has no exponents anywhere in it. It is defined entirely in terms of integers and factorials. This is nice, because frankly, exponents can be tricky, so it is good to define e in terms of really simple operations. Second, this definition converges very quickly. That is, after the first handful of terms, you get very close to our number, 2.72, and after that all the terms are very tiny and only get tinier.
So what we are left with for Euler's identity, in round numbers is this:
2.723.14i = -1
So what? We've talked about all the numbers involved, and it seems no
clearer. What I haven't talked about is the main operation in the
identity, exponentiation, or raising a number to a power.
Now let's talk a bit about the most confusing operation in Euler's formula, exponentiation. How can we even interpret eiπ? Most people have a basic idea of what it means to raise a number to a power, an understanding from grade school math.
32 = 3 × 3 = 9And so on. This is pretty straightforward, nothing mysterious about it. You just take the exponent, the number in the superscript, and multiply the base to itself that many times. Simple, right? Yes, it is simple, but only if the exponent is a natural number, that is, a positive, non-0 integer. I assume that it is not controversial to say, given the above, that:
31 = 3 = 3It is not obvious how we might make sense of exponents that are fractions (irrational real numbers like π) or negative numbers, let alone crazy imaginary numbers like i. As mathematicians, we can decide that that's OK, and the operation of exponentiation is only defined for natural number exponents. There is nothing wrong with that. You keep your math simple, but the price you pay is that your math lacks power and range. It would be nice to see if we can't find a natural interpretation of the more exotic exponents.
Now this gets a little philosophical. When you are very young, math is presented to you as fact. 2+3=5. You can learn the true math you are taught, and you get good at applying it, and you get the answers on the tests right, and you get good grades. Or you fail to learn the math, get wrong answers on the tests, and get bad grades. But as you get older, you come to see math as a bit more fluid. Mathematicians can just make stuff up - as long as it rigorously follows its own rules, and does not contradict anything we already know. So mathematicians were free to just make up new interpretations of exponentiation, as long as the natural number exponentiation we know and love fell out as a special case.
Looking at the natural number, grade-school idea of exponents, there is one important fact that we can observe:
32 × 33 = (3 × 3) × (3 × 3 × 3) = 3 × 3 × 3 × 3 × 3 = 35It should be pretty clear that in general:
ax × ay = ax+yAs long as the base is the same, when you multiply, all you do is add the exponents. Exponentiation takes multiplication problems and turns them into addition problems. Let us think of this as our One True Fact about exponents. Let's grab that fact and not let go. However we extend our exponentiation operation to accommodate exponents other than the natural numbers, let's say it must always be true that ax × ay = ax+y. It turns out that as long as we cling to this One True Fact, it dictates how we should interpret the more exotic, non-obvious kinds of exponents.
While we are at it, it should be clear that a consequence of our
One True Fact is that (ax)y = axy.
That is, when you have something raised to a power, then that whole thing
raised to another power, you just raise the thing you started with to
the product of the two powers:
(23)2 = (2 × 2 × 2) × (2 × 2 × 2) = 23 × 2 = 26
This property of exponents (and their associated inverse function, logarithms, that we will get to later on), that they take multiplication problems and turn them into addition problems, is important, at least historically. Since addition is generally easier to do than multiplication, in the old days before electronic calculators, engineers used to go around with a slide rule sticking out of their shirt pockets. These devices, used in conjunction with a book of tables, allowed people to quickly multiply numbers by adding exponents. For several centuries, anyone who did lots of calculations, whether they were an engineer, a scientist, or a mathematician, used exponents and logarithms to simplify multiplication by turning it into addition.
Right off the bat, let's have a look at 30. You were all probably taught at some point that anything raised to the 0th power is equal to 1, so 30 = 1, but I, for one, was just taught this as a fact to memorize. But now, if we want it to always be true that ax × ay = ax+y, we can see that a0 must always be 1, because ax × a0 = ax+0 = ax no matter what a or x are. So multiplying by a0 can't change the result, so a0 must be 1.
What is a-1? Using our One True Fact,
ax × ay = ax+y, we know that:
a1 × a-1 = a1 + -1 = a0 = 1
So if
a × a-1 = 1
a-1 can only be 1/a.
Similarly:
a2 × a-2 = a2 + -2 = a0 = 1
so:
a-2 = 1/a2
In general, then, a-x = 1/(ax)
What about fractions? Let's start with a simple fraction, 1/2.
Once again, if we insist that ax × ay = ax+y, then:
a1/2 × a1/2 = a1/2+1/2 = a1 = a.
So if a1/2 × a1/2 = a, then a1/2 must be the square root of a. Similarly, a1/3 must be the cube root of a, and in general a1/n must be the nth root of a.
We can also use that consequence of our One True Fact, that is,
(ax)y = axy.
(a1/2)2 = a(1/2 × 2) = a1 = a
We are trying to figure out an interpretation of a1/2, and we
see that when you square it, it equals a,
so it must be the square root of a.
What about fractions with numbers other than 1 in the numerator?
Since any fraction
of integers x/y is just x × 1/y we can see that:
ax/y = a(x × 1/y) = (a1/y)x
In general, ax/y is the yth root of a, to the xth power.
So this covers all possible fractions, or rational numbers. What about irrational reals, like π or √2? I'm going to wave my hands a bit here, and just sort of describe verbally rather than prove mathematically how this would work, using some calculus-like thinking. You may know that you just can't express √2 with any finite fraction. It goes on forever. But, assuming that exponentiation is a continuous function (that is, no sudden jumps, kinks or angles in its graph), we can make an arbitrarily precise guess about a√2.
That is, if you demand accuracy within 1/1000, I can come up with a fraction that is slightly larger than a√2 but within 1/1000 of it, and calculate athat thing, and then come up with another fraction that is slightly smaller than a√2 but within 1/1000 of it, and calculate athat other thing. Then I will have two values, very close together, and we will know that a√2 is somewhere between them. Then if you demand even greater accuracy, say, within 1/1000000, I can do that too. Basically, while I may not be able to directly calculate a√2 exactly, I can zero in on it to any degree of closeness you could demand, which is close enough.
This kind of hand-waving approach would work fine for engineering, but is not what we are looking for as mathematicians. It turns out that the best way to cover all the strange varieties of exponentiation is to redefine it altogether.
e = (1 + 1/n)n as n goes to infinity. So:
ex = (1 + 1/n)nx
as a result of our truth that (ax)y = axy.
Now put x in both the top and bottom of the fraction:
ex = (1 + x/nx)nx
Now that nx appears in both places, as n goes to infinity, nx will just
as well, at the same rate, so we can just simplify:
ex = (1 + x/n)n as n goes to infinity.
We now define ex = limit of (1 + x/n)n as n goes to infinity.
We can derive an infinite series for ex using Pascal's triangle,
and the binomial formula, just as we did above for e itself (i.e. e1):
ex = (1 + x/n)n as n goes to infinity =
1 + x/1! + x2/2! + x3/3! + ...
This is not very intuitively satisfying, since it involved a lot of algebraic trickery, but we can see that it more or less agrees with our elementary school idea of natural number exponents by punching in the first few exponents and calculating the first several terms of each (after that, each term gets so tiny that by five, we are pretty close to the actual answer, although this is less true the bigger the exponent):
e1 = 1 + 1/1! + 12/2! + 13/3! + 14/4! + 15/5! = 1 + 1 + 1/2 + 1/6 + 1/24 + 1/120 = 2.71666…
…which is pretty close to e ≈ 2.71828
e2 = 1 + 2/1! + 22/2! + 23/3! + 24/4! + 25/5! = 1 + 2/1 + 4/2 + 8/6 + 16/24 + 32/120 = 1 + 2 + 2 + 4/3 + 2/3 + 8/15 = 7.2666…
…and my calculator says that e2 ≈ 7.39…, so again, getting pretty close.
e3 = 1 + 3/1! + 32/2! + 33/3! + 34/4! + 35/5! + 36/6! = 1 + 3/1 + 9/2 + 27/6 + 81/24 + 243/120 + 729/720 ≈ 19.41
…and my calculator says that e3 ≈ 20.09
Now we are getting somewhere, since this expression allows us to define exponentiation, ex for any x, using only good old fashioned natural number exponents, the kind that even little kids understand, even if the x is something more exotic, like an irrational real, a complex number, whatever. Moreover, it converges really quickly, that is, after the first few terms, the terms get really small and no longer contribute very much to the total. Note that if we use this formula, but set x = 1, we just get the infinite series definition for e itself. So this formula for ex is the more general formula, with e = e1 falling out as a special case.
I know you aren't supposed to have to know anything about calculus to understand this presentation, but I'm going to go off on a little bit of a calculus tangent here. It's OK if you don't follow it completely, but I will try to set it up for you by doing a criminally oversimplified 90 second calculus course.
Calculus answers two questions. The first involves the slope of a curve. We know that the slope of a line is rise over run. Given any two points on a grid, we can draw a line between them and figure out the slope of that line.
So what about a parabola?
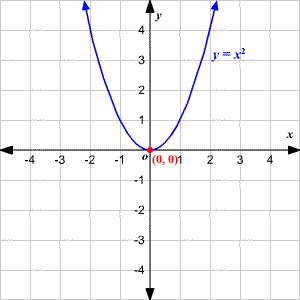
What is the slope of this? Well, obviously it depends on where on the curve were are talking about. It seems intuitively clear that right at the bottom, where the curve hits the origin (0,0) because 02 = 0, the slope is probably 0, a horizontal line.
It should seem pretty clear also that the further out you go from the origin to the right, the slope gets bigger and bigger, as the arms of the parabola get steeper and steeper. The thing is, there is no such thing as the slope of a point, only the slope of a line. What we are asking is, what is the slope of a line tangent to the parabola, at any given point? The answer to this question is clearly different for different values of x. So to answer it, we want a whole new function of x. If the curve of the parabola itself is given by y = x2, we need a new function, called the derivative of y, that when given x as an input, will give us our slope as an output. We write that as y', pronounced "y prime".
Newton and Leibniz more or less independently figured out that to find the slope of a curve at a particular point, you could figure out the slope of line segments whose endpoints were on either side of the point, with the lines getting shorter and shorter. Using the concept of a limit we can say that the slope of a curve at a point is the limit of the slope of such a line segment as the segment gets infinitely short.
It turns out that for our parabola, y' = 2x. That is, the slope of the parabola at any point is just twice whatever x is at that point.
This notion of the slope of a curve sounds all very graphic and geometric, but it is related to the idea of rate of change. That is, if a function tells us that something in the world is changing as a result of something else, the slope of its curve tells us how fast it is changing. The example people always use is that of position, velocity, and acceleration. That is, velocity is a measure of your change of position over time, and your acceleration is your change of velocity over time.
The first question calculus answers is how to find the derivative of a function, that is, a whole new function that tells you the slope of your first function's curve at any point. The second question calculus answers is how to find the area under the curve of a function.
How could we find this area, if we knew the formula that gave us this squiggly line? Let's go back to our parabola again, y = x2.
Newton and Leibniz also figured out that you can approximate the answer by filling in the region with skinnier and skinnier rectangles and adding their areas together. The limit of that sum as the rectangles get infinitely thin and infinitely numerous is your answer. This gives us yet another function of x, called the integral of our original function. You plug in the x at the beginning of your area and the x at the end of your area, subtract, and you have the area of the region you want.
For example, it turns out that the integral of our parabola,
y = x2, is 1/3x3. So if we want to find the
area under the parabola between x=1 and x=3, we find that:
1/3 × 13 = 1/3
1/3 × 33 = 9
9 - 1/3 = 8 2/3
So our area is 8 2/3.
So this is the big reveal, the spoiler of all of calculus. Let's say you have a function, f(x). Let's call it Fred. Let's say you know Fred's integral, that is, another function that tells you the area under Fred. What is its rate of change? What is the slope of the curve that is Fred's integral? It turns out that the answer is Fred. The integral just is the antiderivative. The rate of change of the area under a curve is the same as the curve you started with. Another way of saying this is that if you have a curve that represents Fred's slope over time, that is, Fred's derivative, the area under that curve is Fred itself. The integral and the derivative are inverse functions of each other. The integral of the derivative of Fred is Fred, and the derivative of the integral of Fred is Fred.
Using our old parabola, y = x2, we said that its
derivative is:
y' = 2x
And its integral is:
1/3x3
So we can say that the integral of 2x is x2, and the
derivative of 1/3x3 is also x2.
A bit ago I defined ex. Note that this definition is a function. That is, you give me an x, I'll give you a y, and we can graph this function, just as we did for y = x2 to get our familiar parabola.
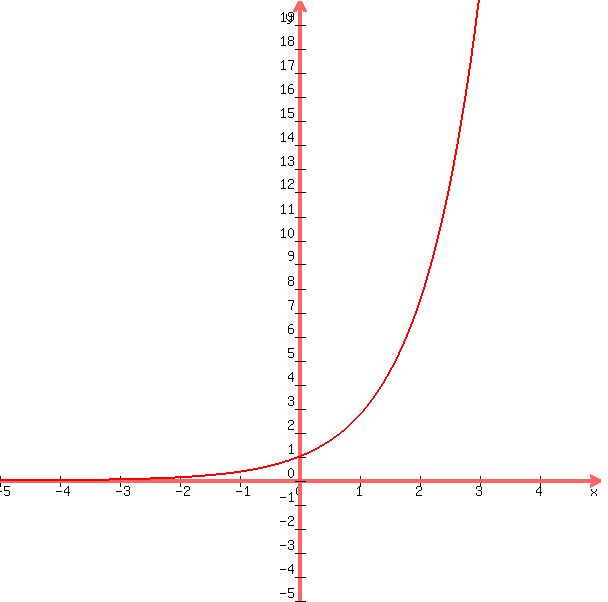
We can
use calculus to show that the exponential function (with an arbitrary
base, i.e. y = bx, with b for "base")
is proportional to its own derivative. That is, if y = bx then:
y' = Cbx
where C is some constant, just a regular old number, that depends on
what we chose as our base, b. It would be natural to want a base
where this proportionality constant C was 1, so that we could
have a simple:
y' = bx
If we could find a base like that, it would seem like nature wanted us
to use it. It would be the natural base. It would make that particular
exponent function a bit freaky, because it would be equal to its own
derivative. That is, all along its length, the slope at any point is
equal to its value at that point. It seems intuitively plausible that
there might only be one function in the universe of which that could
be true. We see above that our friend the parabola does not have this
property, since x2 is certainly not equal to its derivative, 2x.
And because derivatives and integrals are inverse functions,
a function that is equal to its own derivative function would also
have to be equal to its own integral functions. Wild.
Mathematicians, using calculus magic, set this C = 1 and worked backwards to find this natural base, b. When they did this and solved for b, the expression they found was the same thing we recognize as the definition of e that the money lenders had figured out from their interest rate calculations centuries ago, the limit of (1 + 1/n)n as n goes to infinity. So e is this sought-for natural base, and ex is the function that is equal to its own derivative (and integral) full stop.
In fact, using more calculus magic, mathematicians are able to characterize an
infinite series for a mythical function that is its own derivative. When they
do this, lo and behold, it turns out to be equal to the infinite series
definition we already know for ex:
1 + x/1! + x2/2! + x3/3! + ...
I mentioned logarithms before. One way to think of a logarithm is
as a function that is the opposite, or inverse,
of the exponentiation function.
That is, if you have an exponentiation function with a base of 10, then:
y = 10x
So if x is 2, then y is 100:
100 = 102
The associated log function, log(), says that:
log(100) = 2
Similarly, log(1000) = 3, etc.
Since people tend to feel comfortable with base 10, these base 10 logarithms, or common logarithms, were popular before any other kind. By convention, usually log() means base 10. If the exponentiation function asks, "what is the base raised to this power?", the logarithm asks the opposite question: "What power would I have to raise my base to in order to get this?".
Since logarithms and exponentiation are inverse functions of each other,
it is automatically true that (again, assuming base 10, but this is true
for any base):
log(10x) = x (try using x = 2, as per the example above)
10log(x) = x (try using x = 1000, as per the example above)
In general, if you graph a function on a plane, you can see its
inverse function by just flipping your x's and y's, that is, by
rotating the whole curve around the line x=y.
A lot of people have trouble getting their heads around logarithms. Everyone understands exponents, at least to some extent, but their inverse, logarithms, seem tricky. One way to look at them, at least using a base of 10, is to think of them as orders of magnitude. How many digits are there in a given number? Let's say you are talking about someone's annual salary. We could say they make 2, 3, 4, 5, 6, or 7 figures. If you have a six figure income each year, you make somewhere between $100,000 and $999,999. Note that each single bump up in the number of digits means the range we are talking about gets multiplied by 10. The bigger the numbers, the less precise we are. Logarithms are a way of representing multiplying by the base as an addition of one.
It is an accident of evolution that we happen to have 10 fingers,
and thus ended up using a base 10 number system. We have already
seen that, for reasons relating to calculus, and derivatives, integrals,
and whatnot, that the natural base for the exponentiation function is e.
Its inverse function is thus called the natural logarithm function,
and is denoted ln(), sometimes pronounced "ellen". Just as with the
common logarithm, ex asks "what is e raised to the x power",
while ln(x) asks, "what power would I have to raise e to to get x?" So:
ln(ex) = x
eln(x) = x
We can draw ln() by flipping a graph of ex around x=y:
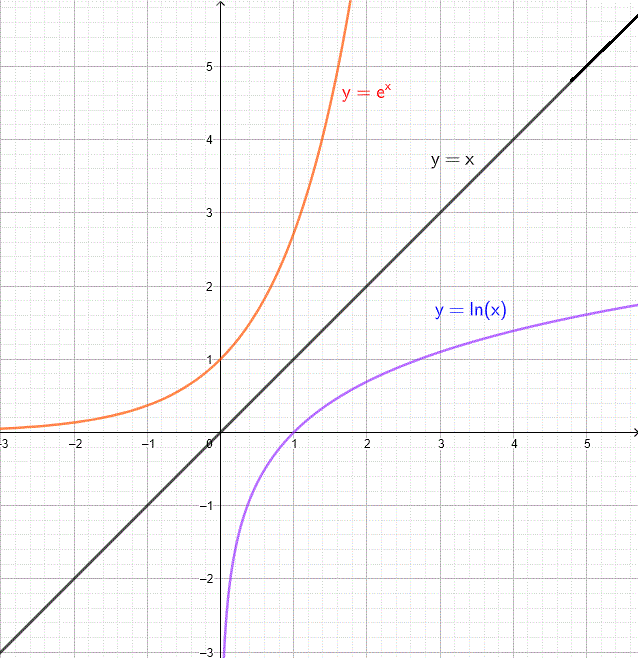
It should be clear that ln(e) = 1, since e1 = e. Likewise,
whether we are talking about log() (base 10) or ln() (base e):
log(1) = 0
ln(1) = 0
since a0 = 1 for any value of a, including 10 and e.
Remember our One True Fact about exponents, that:
ax × ay = ax+y
That is, the way exponentiation has a way of turning multiplication
problems in to addition problems. Let's think about what that means
for logarithms. Let's do an example, keeping it really simple, with
base 10 and integral powers of it. We know that, for instance,
10000 = 104
1000 = 103
10 = 101
So since:
10000 = 1000 × 10
104 = 103 × 101
and this obeys our One True Fact about exponents, because 4 = 3+1. We know
that
log(10000) = 4
log(1000) = 3
log(10) = 1
So we see that:
log(10000) = 4 = log(1000) + log(10) = 3 + 1
As I said, logarithms take some getting used to, but it should seem plausible
to you, if not obvious, that:
log(mn) = log(m) + log(n)
and likewise:
ln(mn) = ln(m) + ln(n)
The base, 10 or e, or 8 or 23, should not matter with regard to this
property.
As I mentioned earlier, in past generations, people who had to do a lot of calculating used logarithms to turn multiplication problems into addition problems.
A bit ago I defined ex in two different, but equivalent, ways. That is all we need for Euler's identity, but we should briefly talk about how to extend exponentiation to bases other than e. Since ex and ln(x) are inverse operations, a = eln(a). If we think of ln(a) as being the answer to the question "What power do we have to raise e to in order to get a?", then we raise e to that power, we get a.
Remember also that
(ax)y = axy
Therefore, if a = eln(a) and we raise each side to power x:
ax = (eln(a))x = ex ln(a)
So now we have defined an exponentiation function for any base (a) in terms of the one we already defined for base e.
When logarithms were first discovered, they were thought of as just the inverse of exponentiation. Just say ln(x) is the inverse of ex. But considering the logarithm function, ln(), as a function in its own right, what is its derivative, the function of x that shows its rate of change, or slope at any point? Using calculus, we know how to flip a function along the line y = x to graph its inverse, and calculate the derivative of this inverse. Just using the one fact that ex is its own derivative, we can show that the derivative of it inverse, ln(x), is the function y = 1/x. Importantly, this means that the antiderivative, or integral, of 1/x is ln(x). For various reasons, it took a long time after the invention of calculus to figure out the integral of the function y = 1/x. It might not sound like much, but this was a mystery, so it was a kind of big deal, mathematically, when they finally figured it out.
[e: p. 156] says that Euler put both functions on equal footing by
defining them independently:
ex = (1 + x/n)n as n goes to infinity
ln(x) = n(x1/n - 1) as n goes to infinity
but note that these are easily shown to be inverses of each other.
I assume you remember trigonometry? Remember sine, cosine, and tangent? I'm going to do a brief review here. If you add up all three angles in any triangle, they add up to 180°. A right triangle is one that has a 90° angle as one of its angles, so that leaves only 90° to divide between the other two angles. Trigonometry deals a lot with right triangles.
You probably remember that the longest side of a right triangle is the one opposite the right angle, and is called the hypotenuse. Since the two non-right angles have to add up to 90°, if you are dealing with a right triangle and you know the degrees of one of the other angles, you can easily figure out the degrees of the other one too. So if the right angle is, of course, 90°, and one of the other angles is 27°, you know that the other angle has to be 63°.
If I draw this right triangle, with angles of 90, 27, an 63 degrees, you can't tell how big it is, what units I am using (inches, miles, etc.), but the ratios of the sides to each other are definitely going to be whatever they are regardless of the size or the units. That is, if you know that one of the angles is 27°, you might not know how long the side opposite that angle is, but you can certainly know for sure that the ratio of that side over the length of the hypotenuse is whatever it is. You may even remember that for any angle, the names we give for these ratios are as follows:
| sine | opposite/hypotenuse |
| cosine | adjacent/hypotenuse |
| tangent | opposite/adjacent |
For instance, we can say that the sine of 30° is 0.5 (one half), or the tangent of 41° is about 0.87.
Look at the first two of the three ratios, or fractions there, the sine and cosine. We won't talk about tangent anymore. First, since the hypotenuse is always going to be the longest side of a right triangle, the bottom, or denominator, of the sine and cosine is always going to be greater than the top, or numerator. This means that sine and cosine are always less than 1 (well, almost always. More on that in a bit). Second, the arithmetic would be a lot easier if we limited ourselves to right triangles with a hypotenuse of 1, in which case the denominator is just 1, and the sine is just the outright length of the opposite, and the cosine is just the length of the adjacent.
So instead of thinking of our right triangle as just floating in space, think of it as inscribed in a unit circle centered on the origin of a Cartesian grid.
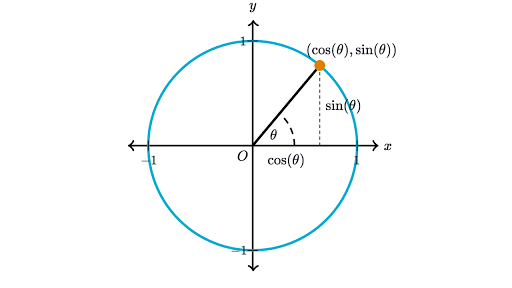
The radius of our circle is 1 (that's what we mean by "unit circle"). Think of the radius sweeping around the circle like the hand of a clock, but counterclockwise, starting at three o'clock, that is, pointing straight out in the positive direction along the x axis. Now look at the point on the circle that the radius hits as it sweeps around, and the angle that the radius makes with the x axis. Drop a vertical line from that point to the x axis, and we have a right triangle. The radius of the circle is the hypotenuse of this right triangle, and that hypotenuse is always 1. Moreover, the (x,y) coordinates of the point on the circle that the radius hits are the cosine and sine of the angle that the radius makes with the x axis. Note that the x and y are always guaranteed to be less than 1, except when the radius lies exactly along the x or y axis, in which case we don't have a triangle at all.
In trigonometry, the tangent is the ratio of the opposite over the adjacent sides of an angle in a right triangle. Do you know the other meaning of the word "tangent" in geometry? If you have some arbitrary curve describing a function, and a straight line comes along and touches that curve at exactly one point, just a little kiss, that line is a tangent. Sometimes we speak non-mathematically about someone going off on a tangent. That is, a conversation was going along on a certain track, and someone touched on something ever so briefly, but took the whole thing off in a different direction.
So why do we use the same word, "tangent", to mean a line that intersects a function at just one point, and also to mean the opposite over the adjacent? Look at the unit circle, and a point on it, and draw a line tangent to the circle that hits it just at that point. It turns out that the length of the segment of that tangent line between the point where it hit the circle and the point where it hits the x axis, is going to be equal to the opposite over the adjacent of the angle the radius makes with the x axis. The proof is actually pretty simple.
There is one more twist in the way we do trigonometry in more advanced math. I keep saying things like 90°, 180°, and 27°. We all know that there are 360° in a circle. Why? Who decided that we should divide circles into 360 of anything? Blame the Babylonians thousands of years ago. Wouldn't 100 be sort of easier to work with? Shouldn't there be something like a metric system for angles?
Well, it turns out there is, but you're not going to like it, at least not at first. To make the arithmetic work out more easily, mathematicians do not like to divide circles into 360°, but they also don't like to divide it into something you might expect, like 100°. No, they invented a new unit of angle measure called a radian. They decided that things work out most easily for their purposes if the angle measure in radians is the same as the length of the corresponding arc of a unit circle. Got that?
If a unit circle has a radius of 1, it has a diameter of 2, and a circumference of 2π. So the angle measure of a complete circle, instead of being 360°, is 2π radians, about 6.28. Half a circle, instead of being 180° is π radians. A right angle, or quarter of a circle, instead of being 90°, is 1/2 π radians. One radian is about 57°. One of the annoying things about radians is that there is not an integer number of them in a circle, since 2π is not an integer.
| 360° | 2π radians |
| 180° | π radians |
| 90° | 1/2π radians |
| 45° | 1/4π radians |
| ~57° | 1 radian |
But, as I said, a lot of math gets easier if we use radians, and even though it seems like comparing apples and oranges, things work out nicely when the angle measure is numerically equal to the arc length. In general, in calculus when they talk about angles it is assumed that the units are radians. It's just a small change of convention, there is nothing really conceptually different about using radians instead of degrees.
Let's look at just sine and cosine. The sine of any angle measure, as I said, is the y coordinate of the point on the unit circle pointed to by that angle, and the cosine is the x coordinate. Feed an angle measure (in radians!) in, get an x or y coordinate out. Let's look at sine first, thinking of it as a function, like y = x2, except this function is y = sine of x, written as sin(x).
We start with a Cartesian grid, with an origin. Normally, we would mark off units along the x axis, 1, 2, 3, ... but since our x is an angle measurement in radians, I'm going to mark it off in units based on π.
Now let's fill this in with a graph of the function sin(x). Sine is the y coordinate of a point on the unit circle, so it can never get bigger than 1 or smaller than -1, so we know our function is going to be bounded by those values on the y axis.
Looking at our unit circle, what is the y coordinate of an angle of 0 radians? Since that point lies right on the x axis itself, the y coordinate is 0, so sin(0) is 0.
Note that now that we are talking about the unit circle, and not just triangles, we can talk about all kinds of angles. We are no longer limited to angles of less than 90°. So let's look at a 90° angle itself, or as we are calling it now, a π/2 radian angle. What is its sine, or the y coordinate of the point on the unit circle that is hit by a radius at a right angle to the x axis? In that case, the radius lies right on the y axis, and the y coordinate is 1. So sin(π/2) = 1.
An angle of π radians takes us halfway around the circle, to the point (-1, 0), so sin(π) = 0. 3/2π is 3/4 around, at the point (0, -1), so sin(3/2π) = -1, and all the way around, 2π, brings us back where we started, so sin(2π) = 0. If you keep going, you will see that 2.5π gets us right back to (0, 1), so sin(2.5π) = 1.
It should be clear that sine is a periodic function, which means that as we keep going higher in our x values, we will keep repeating the same y values forever, as we keep going around and around our unit circle. Looking at what I've plotted so far, it looks like the sine function zig-zags forever around the x axis, but the curve is smoother:
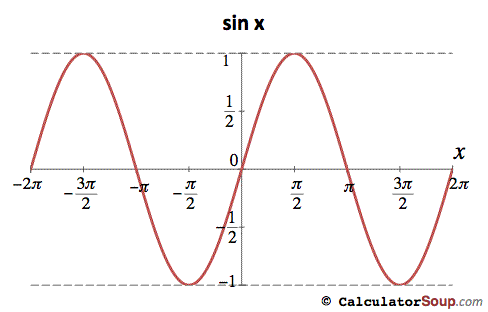
This curve is called a sine wave. Since when the sine gets big the cosine gets small, but they are essentially copies of each other, if we were to plot the cosine on the same grid, we would just slide the sine function over π/2 radians.
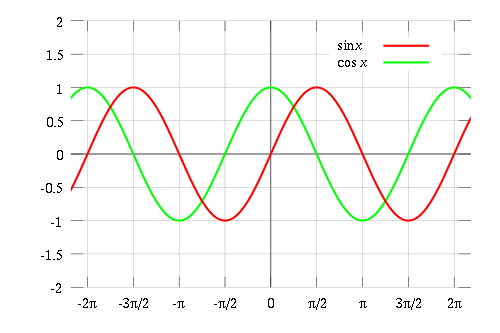
We say that the sine and cosine functions are 90° out of phase, or rather π/2 radians out of phase.
OK, so now we are thinking of sine and cosine as mathematical functions that we can plot on a Cartesian plane, and we are using radians as our units for measuring angles. The last thing I want to tell you about trigonometry is another way of representing the sine and cosine functions.
Soon after calculus was invented, mathematicians found out a lot of techniques for dealing with functions that are polynomials. If you don't know what that means, never mind, but sine and cosine are not polynomials. They are a little weird. So early on, some mathematicians, using calculus magic, figured out how to rewrite the sine and cosine functions as infinite sums, that while infinite, are polynomials. So far, I have tried to make this whole talk understandable to anyone paying attention, and I hate that at this point I'm going to have to say, just trust me. It would be a whole other presentation to explain the steps, and if you are really interested, there are some Khan Academy videos, Wikipedia entries, and stuff like that. Start by googling "Taylor series" and/or "Maclaurin series".
So here it is, as discovered by those early calculus people:
sin(x) = x - x3/3! + x5/5! - x7/7! + ...
cos(x) = 1 - x2/2! + x4/4! - x6/6! + ...
Keeping in mind that our x's here are radians, sure enough, if you
plug in numbers and plot out the results, you end up with the sine and cosine
wave functions.
So let's just park these to so-called infinite sums for sine and cosine
aside for a moment, and we will use them soon, but for now we will
return to the exponentiation function, for which we also already have
an infinite sum representation.
So we have a definition of exponents with e as a base in terms of
an infinite sum, from the binomial formula:
ex = 1 + x/1! + x2/2! + x3/3! + x4/4! + ...
So what if we just use ix instead of x in that expression? We would have:
eix = 1 + (ix)/1! + (ix)2/2! + (ix)3/3! + (ix)4/4! + ...
Note that in general, (ab)x = axbx. That
means that all the terms in this expression that look like this:
(ix)k
could be rewritten like this:
ikxk
So then we have:
eix = 1 + ix/1! + i2x2/2! + i3x3/3! + i4x4/4! + ...
But remember that progression we wrote out before of successive powers of
i? If we perform substitutions using that, we get this:
eix = 1 + ix/1! + (-1)x2/2! + (-i)x3/3! + (1) x4/4! + ...
eix = 1 + ix/1! - x2/2! - ix3/3! + x4/4! + ...
So now every other term in this infinite sum has i as a factor (the
even ones), and every other term does not (the odd ones).
If we group all the regular non-imaginary terms first,
then factor out the i from the imaginary terms and group them second,
we get:
eix = (1 - x2/2! + x4/4! ...) + i(x/1! - x3/3! + x5/5! ...)
Remember those infinite sums expressions for sine and cosine I introduced
a bit ago and told you to park aside for a moment?
Well it turns out that the first part, the real part:
1 - x2/2! + x4/4! ...
as was well known in Euler's time, is just the infinite sum that is
equal to cos(x), and the second part, the part in the parentheses:
x/1! - x3/3! + x5/5! ...
is just the infinite sum that is equal to sin(x). So what we are
left with is:
eix = cos(x) + i sin(x)
Now if we let x = π, we get eiπ = cos(π) - i sin(π).
Recall that we are using radians as our angle units, and a complete
circle is 2π radians around, so π is exactly half a circle, or 180°.
The point on the circle halfway around lies on the x axis at -1, so its y
coordinate is 0, and its x coordinate is -1. Therefore:
cos(π) = -1
sin(π) = 0
and thus:
we get eiπ = cos(π) - i sin(π) = -1 - i0 = -1.
Similarly, WMCF p. 445 shows that since f(y) = cos(y) + i sin(y) and eyi have the same derivatives at 0 for all infinite derivatives, their Taylor series are identical, therefore they must be the same function. But even this entails knowing the derivatives of trig functions: see Purcell p. 364 for proofs of these.
Yay! We've done it! Euler's identity is proven! That works out algebraically, but it seems almost magic, like some sleight of hand trick: suddenly trig functions just pop out of the algebra when we collect terms, the i drops out when we multiply it by 0, and viola! we have our -1. Let's give it all a more intuitively satisfying geometric interpretation.
OK, so that's a bit weird - we have a new way of expressing i, albeit one
that involves i on both sides of the equals sign. But what if we now raise
both sides to the power of i? We get:
(eiπ/2)i = ii
But remember that whenever we raise a power to another power, we just
multiply the exponents. But also remember that
i × i = -1. so:
(eiπ/2)i = eiiπ/2 = e-π/2
and that is just roughly 2.72-1.57 = 0.21
Strange but true: ii is about one fifth.
Sometimes the key to mathematical insight is just a matter of having the right metaphor or image. Consider the good old number line:
This is a nice way of visualizing numbers and their relations to each other. You can think of multiplying a number by stretching the number line, or rather, stretching a new number line superimposed on the old one. To multiply by a negative number, you have to flip the number line, or perhaps rotate it by 180°. In particular, multiplying by -1 means just a flip or rotate, with no stretching.
Sometime roughly around the 1700s, mathematicians started to notice some similarities between operations on complex numbers (that is, numbers involving i, the square root of -1) and totally different trigonometric operations on regular numbers (like sine and cosine). Eventually, they exploited this and came up with a neat visual way of representing complex numbers. They invented the complex plane. A complex number is one of the form a + ib, where a and b are reals. By convention, the horizontal axis represents the real part, a, and the vertical axis represents the imaginary part, b.
Note that this is different from the way we often use a Cartesian plane in algebra, where we graph a function. In that case, the horizontal (x) axis is the independent variable, and the vertical (y) axis is the dependent variable. That is, x is the input and y is the output of some function, and the curve or line we draw illustrates how the function works.
In the case of the complex plane, we are using the whole plane, both dimensions, just to show numbers, without any function involved. For the real numbers, you need an infinite line to show them all, but for the complex numbers, there is a whole infinite plane's worth of them.
Some ways of visualizing math are better than others, because the picture really reflects the relations between the numbers in a simple truthful way. The complex plane is so good at this, it seems pretty clear that it is just The Right Way of visualizing complex numbers.
Let's start with multiplication. On the old real number number line, if we multiply 3 by -1, we start at 3, and flip or rotate 180° and end up at -3. Do we flip, rotate around counterclockwise, or out from the plane? It doesn't matter how we visualize the 3 in transit to -3, as long as we end up flipped by 180°. So let's just say multiplying by -1 is rotating counterclockwise 180°. Since i is the square root of -1, if we multiply 3 by i twice, we should get -3:
If we show 3, 3i, and -3 on the complex plane, it should be clear that if multiplying by -1 is rotation by 180°, then multiplying by i, the square root of -1, gets you halfway there, and thus is rotation by 90°.
We can keep going. Multiply -3 by i, and you get -3i, another 90° counterclockwise turn from -3. Once more, and -3i × i = -3 × i2 = -3 × -1 = 3, which brings us right back to where we started, 3. This makes sense. Since -1 × -1 = 1, if you multiply anything by -1 twice, you get your original number back, and since i × i = -1, if you multiply any number by i four times, you get your original number back. In the same way, if you rotate a point 180° twice, you end up where you started, but rotating by 90° four times does the same thing. So this way of visualizing complex numbers, and this "rotate by 90° to multiply by i" operation on the complex plane, fits perfectly with that sequence I talked about back when I first discussed i.
This trick works for any complex number at all. (1.3 + 5.7i) × i = 1.3i + 5.7i2 = -5.7 + 1.3i, which is just the original number, 1.3 + 5.7i, rotated counter clockwise 90°. It should be clear that multiplying by -1 also works: (1.3 + 5.7i) × -1 = -1.3 - 5.7i, which is just the original number 1.3 + 5.7i, rotated around the origin by 180°.
When you multiply two complex numbers, you use the good old FOIL
method you would when multiplying in algebra:
(a + bi) × (c + di) =
ac + adi + bci + bdi2
But wait! That last term has i2 in it, and i2 = -1!
So this whole thing is really:
ac + adi + bci - bd
And when we collect the real terms and the imaginary terms together
and factor out the i, we get the final resulting complex number:
(ac - bd) + i(ad + bc)
OK, so that was some cute algebra, but the result doesn't seem to show us anything terribly interesting about the complex number we get when we multiply two other complex numbers together. But there is something terribly interesting about two complex numbers multiplied together! To see what it is, we are going to have to think about points on a grid in terms other than our traditional x,y coordinates.
In general, for any Cartesian grid, if I put a point anywhere on it, we can identify that point using only two numbers: the x coordinate and the y coordinate. These are the ordinary Cartesian coordinates. But there is another way we could specify the point using only two numbers, that is, using its so-called polar coordinates. When we use polar coordinates, the two numbers we use are the angle the point makes with the x axis, and the distance the point is from the origin.
If we pick two arbitrary points on the complex plane that we want to multiply, and notice for each of them the angle they sweep out and the distance each one is from the origin, and do the same thing for the number we get after we multiply them together, that is, their product, we get a result that you might not expect. It turns out that the product is a point whose angle from the x axis is the sum of the angles of the two factors, and whose distance from the origin is the product of the distances of those of the two factors.
Unfortunately, this is one of those situations where I have to wave my
hands and say "trust me", but I can get us part of the way there. I'm
going to rush through this, so if you don't catch all of it, don't worry
too much. Think about our polar coordinates,
with a little trigonometry mixed in. We can take our generic
complex number, x = a + bi, and represent it not in terms of
a and b, but in terms of the angle it makes with the X axis, A, and the
distance from the origin, r1. In this case, r1 is the hypotenuse of
a triangle, and our real part, a, the horizontal component, is
cos(A) × r1, and the imaginary part, b, the vertical component is
sin(A) × r1. Then we can rewrite our original complex number,
a + bi, like this:
x = (r1 × cos(A)) + i(r1 × sin(A))
We can undistribute the r1 out and put it outside and get:
x = r1(cos(A) + i sin(A)).
So let's say we want to multiply our x by a whole different complex
number, y, that we've done the same thing to in terms of its representation
on the complex plane. Let's say that y is the complex number at angle B,
and at a distance r2 from the origin. so:
y = r2(cos(B) + i sin(B))
Just like x, but with different values. Then if we actually do all the algebra
to multiply these two things together using FOIL, we get this mess:
xy = r1 r2 [(cos(A) cos(B) - sin(A) sin(B)) + i(sin(A) cos(B) + sin(B) cos(A))]
Here is where the hand-waving comes in. It turns out that there is a
couple of formulas called the addition formulas for sine and cosine,
and they say the following:
cos(x + y) = cos(x) cos(y) - sin(x) sin(y)
sin(x + y) = sin(x) cos(y) + sin(y) cos(x)
The proofs of these have a bunch of steps, but it isn't all that conceptually tricky, if you are good at geometry. If you are interested, there is a decent graphical presentation online, and if you stare at it for a while, it actually begins to make sense.
So we can rewrite the messy product of our complex numbers:
xy = r1 r2 [(cos(A) cos(B) - sin(A) sin(B)) + i(sin(A) cos(B) + sin(B) cos(A))]
like this:
xy = r1 r2 [cos(A + B) + i(sin(A + B))]
It should be clear now that this, in turn, is the polar representation of some point on the complex plane whose distance from the origin is r1 × r2, and whose angle from the x axis is A + B.
On the other hand, if you don't believe the addition formulas for sine
and cosine, but you do accept the equation above,
eix = cos(x) + i sin(x), we can show
the same result. Let's go back to our two arbitrary complex numbers that
we want to multiply together:
(a + bi) × (c + di). Now, using our
polar way of writing these, let's say:
a + bi = (r1 × cos(A)) + i(r1 × sin(A))
c + di = (r2 × cos(B)) + i(r1 × sin(B))
We can undistribute the distances, r1 and r2, to get:
a + bi = r1 × (cos(A) + i sin(A))
c + di = r2 × (cos(B) + i sin(B))
Since
eix = cos(x) + i sin(x) we can say:
a + bi = r1 eiA
c + di = r2 eiB
Now what happens when we multiply these together?
(r1 eiA) × (r2 eiB) =
(r1 × r2) × (eiA × eiB)
We know already that when we multiply two numbers together that are
a base raised to different powers, we just add the exponents. So that
second parenthetical bundle, (eiA × eiB)
= eiA + iB = ei(A + B). So now, at last we have:
(a + bi) × (c + di) =
(r1 × r2) ei(A + B)
which is the complex number a distance from the origin of
(r1 × r2), and an angle from the x axis of A + B.
This is a big deal. We have again turned a multiplication problem into an addition problem. An immediate consequence of this is that if you square a complex number, the result is a number with twice the angle of the number you started with. If you cube a complex number, you get a number with three times the original angle. And so on.
If we draw a unit circle on the complex plane, centered on the origin, there is an infinite number of complex numbers that lie on that circle, but they all share one property in common: they are all 1 away from the origin. That means that when you multiply any of them together, the distance of the product from the origin is just 1 × 1 = 1 away from the origin too, so the numbers just chase each other around the circle. Multiplying any two numbers on that circle will yield some other number on the circle. All you have to do is add the angles of the factors together, and that's your angle of the product.
Based on this fact, we notice something convenient about raising complex numbers on this unit circle to integer powers. If you square a complex number on this circle, the result is just the point whose angle is double the angle of the number you started with. If you cube a complex number on this circle, the result is just the point whose angle is three times the angle of the number you started with. If you raise such a number to the 23rd power, the resulting product has an angle 23 times the angle you started with.
OK, so let's bring all this back to Euler's identity. Start with:
ex = (1 + x/n)n as n goes to infinity
and let x = iπ:
eiπ = (1 + iπ/n)n as n goes to infinity
Note that the part inside the parentheses, 1 + iπ/n, is a complex number whose real part is just 1, and whose imaginary part is iπ/n. As n gets bigger and bigger, the imaginary part gets smaller and smaller, so the whole thing gets closer and closer to just 1, and its distance from the origin gets closer and closer to 1. So the bigger n gets, the closer 1 + iπ/n gets to being on that unit circle.
So now when we raise that to a high power, the distance remains 1,
and the result is going to also be somewhere on that unit circle, but
where? How far around the whole circle will we end up? Since we have
(1 + iπ/n)n
we are multiplying a complex number on the unit circle to itself
n times, so our result will also be on the unit circle. We just need
to know how far around the circle. We are adding n angles together,
so we need to know how big each of those angles is. We know that the
cosine is the real part, which is 1, and the sine is the imaginary
part, π/n.
What can we say about the angle whose sine is π/n as n goes to infinity? First of all, we know that π/n is going to get very very small, so the sine of our mystery angle will get small. But there is something else worth noticing about the angle as its sine gets infinitely small. The smaller the sine gets, and the smaller the corresponding angle gets, the triangle inscribed in the unit circle gets to be a tiny sliver lying along the x axis. As this happens, that y coordinate, the sine, the side of the triangle opposite the ever-smaller angle, gets infinitely close to being the same as the arc length of the circle swept out by that angle. Since we are using radians, by definition the arc length is numerically the same as the angle measure. This means that we can say that as n gets infinitely huge, the angle gets small, but also the angle gets more and more equal, infinitely equal, to the sine itself, or π/n.
So we are adding n angles of π/n each,
giving us a final angle of n × (π/n) = π.
Since, in radians, a circle is 2π all the way around, the point on the
unit circle at angle π is exactly halfway around, at -1. So
finally, we have:
eiπ = (1 + iπ/n)n as n goes to infinity = -1.
Mathologer: e to the π i for dummies (16 minute video).
An intuitive explanation of Euler's formula without ever
mentioning trig functions.
Proving the Most Beautiful Equation Bob Ross Style (14 minute video)
Pretty good explanation of Euler's identity (although not quite
as easy to follow as it pretends to be!)
Imagining Numbers: (particularly the square root of minus fifteen) by Barry Mazur:
A delightful little book about the history of imaginary numbers and how we might
conceptualize them. Discusses the creative and philosophical foundations of
mathematics itself.
e: The Story of a Number by Eli Maor: Really a history of
not just e but of calculus. Lots of anecdotes and context.
Where Mathematics Comes From by Lakoff & Nuñez:
Very conceptual explanation of the way our minds conceive of math,
and why some ways of thinking about it work better than others.
Trigonometry: A Very Short Introduction by Glen Van Brummelen